Historically, many believed that the end goal of multiplication was long division. In fact, the division algorithm was not even taught to students until they reached college because it was considered to be too complicated for most.
Today, teachers try to help students learn the algorithm by giving them mnemonics to remember the process of long division. For example, teachers use phrases such as “Daddy, Mommy, Sister, Brother” or “Dirty Monkeys Smell Bad” to remember the process: Divide, Multiply, Subtract, and Bring Down (DMSB).
While it is regularly taught in elementary math classes, students truly do not need to learn how to divide by two- or three-digit numbers on paper because they will rarely use it in real life. In fact, there is not a single advanced math program that requires students or employees to solve, with paper and pencil, long division problems involving two- and three-digit division. Some authorities suggest that teachers continue to teach long division simply because it is a traditional skill. But if that is the case, why do we not still teach students how to solve square roots using paper and pencil?
An Alternate Algorithm
Instead of spending valuable educational time teaching this antiquated algorithm, perhaps we should focus on using the short division algorithm for solving division problems with single-digit divisors, removing all the extra steps that the DMSB algorithm requires.
How It Works
As we work through the steps of the short division algorithm, let’s use the example of 471 ÷ 3.

The first step in this example is to divide 4 hundred by 3, which is 1 with a leftover or remainder of 1. So, the first digit of the quotient, 1, will be written above the line in the hundreds place. The 1 left over is recorded as a little 1 in front of the 7 inside the division house.
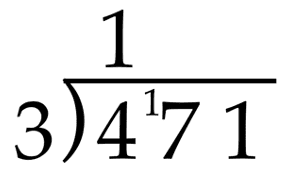
Now, we have 17 tens divided by 3, which is 5 tens. How many are left over? This doesn’t have to be complicated. We know that 3 x 5 is 15, and the difference between 15 and 17 is 2. So, we have 2 tens left over. We can notate this by putting the partial quotient of 5 in the tens place above the line and writing a little 2 next to the 1 inside the division house, as shown below.
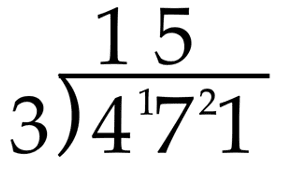
Finally, we have 21 divided by 3, which is 7. We will notate that final 7 on the line and see that the quotient for 471 ÷ 3 is 157.
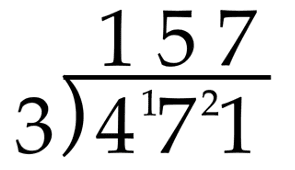
Another Example
Let’s try another one: 8053 ÷ 9.
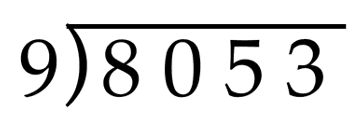
If we look at the thousands place of the dividend, we see that 8 is less than the divisor of 9. So, we need to look at the first two digits of the divided, 80 hundred. Dividing 80 hundred by 9 is 8 hundred with 8 hundred left over. We will notate that by writing an 8 in the hundreds place on the line and recording the leftover 8 hundred in front of the 5 ten inside the division house.
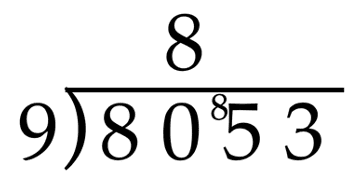
Next, divide 850 by 9, and we have 9 tens and 4 tens left over. Again, we will notate that by writing the 9 in the tens place of the quotient and the remaining 4 tens in front of the 3 in the divisor inside the division house.
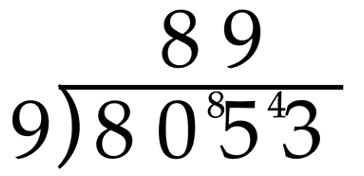
Finally, 43 divided by 9 is 4 with a remainder of 7, giving the final quotient of 894 r7.
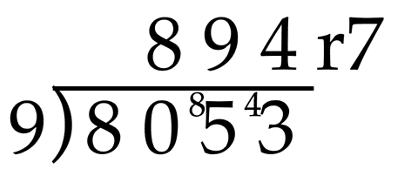
After working through a few of these problems, students see the pattern and can quickly and easily solve short division problems without having to remember an algorithm or use a lot of paper to write each step of the long division process.
Importance of Remainders
Students need to know what to do with and how to apply remainders as they consider the question being asked. Below are five word problems that involve the same numbers. However, all the answers will be different! Find the answers:
- Thirteen students are attending a concert. How many cars will be needed if four students can fit into a vehicle?
- Paulette wants to plant 13 flowers. She needs to have four flowers in each row. How many rows can she plant?
- Four students need to split $13 evenly. How much money does each student get?
- There are 13 candy bars that will be divided among four students. How much money does each student receive?
- Jack has 13 cookies to put in bags that hold 4 cookies. If he can eat the leftover cookies that do not fill the bags, how many cookies can he eat?
Each of these problems involves the same numbers: 13 and 4. Every one of them requires division. However, the solutions differ: 4, 3, $3.25, 3-1/4, and 1, respectively.
These types of problems are often on tests. Notice they require the student to apply arithmetic and thinking skills to solve, not an algorithm to follow.
Student Frustrations with Long Division
Not only do students struggle to remember the process for solving long division problems, but they experience other frustrations as well. They struggle with keeping their columns lined up correctly, potentially causing them to get the wrong answer.
But the biggest frustration students experience in long division is the guessing. If the student is given the problem 2479 divided by 37, what is the first number of the quotient? If the student determined that it is 8 since 24 divided by 3 is 8, they would find that they were wrong. Even putting a 7 in the hundreds place would be incorrect. For this problem, the first digit of the quotient is 6. Oftentimes, students get frustrated because they must continually make educated guesses and then erase their wrong choices.
Summary
Long division is quickly becoming an obsolete skill to learn. In fact, students with learning struggles should not even be taught the long division process. That being said, if long division must be taught, students should first learn the short division process. Then, the traditional long division algorithm will make a lot more sense.
Let’s reduce the strain and frustration our students experience by using the short division model, as it is easier to understand and useful in everyday life.
If you are interested in helping your students excel in mathematics by helping them understand and not just memorize algorithms, contact us to see how you can get RightStart Math into your classroom!
