For many children, multiplication causes a mathematical collapse. What is the reason? They are required to memorize 100 or more multiplication math facts. As instructors, we must first teach our students what multiplication is before expecting them to memorize the facts. Then, we need to use good research-based approaches that will reduce the burden of memorizing numerous multiplication math facts.
What is Multiplication?
Many times, we teach multiplication as repeated addition. However, this limited view does not work when multiplying fractions and decimals.
One essential application of multiplication is finding area. So, let’s use the array model (arranging items in rows and columns) to help students understand multiplication. Start by having the student build three rows of six objects, which is 6 multiplied by 3, or using Montessori terms, “Six taken three times.” The student can clearly see that “six taken three times” gives a product of 18 simply by looking at the array.
Different Interpretations of Math Facts
Multiplication problems can be viewed differently. When looking at 6 × 3, some can think of it as 6 groups of 3. However, a better interpretation is to think of it as 6 repeated 3 times. Why? Because it is more consistent with the rest of arithmetic. When we add 6 + 3, we transform 6 by adding 3 more to it. As we subtract 6 – 3, we transform the 6 by decreasing it by 3. When we divide 6 by 3, we transform the 6 by dividing 6 into 3 groups or dividing 6 into groups of 3. Therefore, for consistency, we should consider 6 × 3 as starting with 6 and transform it by duplicating it 3 times.
This interpretation can also be used in the Cartesian coordinate system. We can represent 6 × 3 in an array of 3 rows of 6, similar to plotting the point (6, 3) on a grid, where 6 refers to the horizontal number, and 3 refers to the vertical number.
Math Fact Instruction Missteps
Rote Memorization
Students are often encouraged to learn multiplication math facts by rote, which many students find overwhelming. Why? They have already learned that 6 and 3 is 9. But suddenly, now it is 18. Instead of just learning multiplication math facts from 1 × 1 to 10 × 10, students are further burdened by extending the number of facts from 1 × 1 to 12 × 12, which adds another 44% more math facts they need to memorize. This heavy load can be reduced by teaching students strategies to quickly calculate 11s and 12s. For example, they can solve 12 × 3 in two steps:
(10 × 3) + (2 × 3) which is 30 + 6 = 36
Songs and Rhymes
Many teachers use songs or rhymes to help their students learn the facts, another misplaced strategy. One disadvantage to this strategy is that the child must sing through the entire song to get the answer they need. A second disadvantage is that the brain must transfer the song or rhyme information from the language part of the brain to the math part of the brain, increasing processing time.
Pictures and Images
Yet another instructional misstep is teaching facts through pictures, one picture for each multiplication math fact. For example, to help the student learn and retain 4 × 4, one image shows a 4-wheel-drive truck. Then, the child is told that the driver must be 16 to drive. When I saw this, the legal driving age in North Dakota was 14. Does that mean that in North Dakota, 4 × 4 is 14? On a serious note, unfortunately, pictures can delay math fact fluency as the student mentally retrieves unrelated images to mathematical concepts.
Skip Counting
A commonly used instructional strategy is to teach children to skip count to learn the facts. However, when children learn to skip count, they often end up just counting on their fingers to get to an answer. I once saw this strategy used in a school in England. The result was that the students became quick at counting but did not master the facts. It just became a procedure for them to memorize.
A Common Misconception about Math Facts
One common misconception about multiplication is the belief that a product is always greater than the factors. However, consider 7 × 1. In this case, the product is equal to one of the factors, not greater than.
Another example of this is when multiplying by zero. For example, 257 × 0 gives the product of 0, which is less than 257.
Finally, the product is always less than either fraction when multiplying proper fractions. Consider ½ × ½ is ¼, which is less than ½.
Superior Instructional Strategies
Commutative Property
We can reduce the burden of memorization by helping our students understand the commutative property. Isn’t it amazing that 6 × 4 is the same as 4 × 6? By introducing this property, students only need to learn 55 math facts rather than 100 (when using a 10 by 10 table).
Of course, for most students, learning the 1s multiplication math facts is easy. For example, the student can understand that 1 × 8 is 1 repeated 8 times, which is 8. Then, when using the commutative property, 8 × 1 is also 8 or can be understood as 8 taken 1 time. The multiples of 2s are easily known from the addition math facts. For example, 5 × 2 is the same as 5 taken 2 times or 5 + 5. Simple enough. Finally, the multiples of 10 are also easy, as they are learned as they work on place value ideas. That leaves only 28 more multiplication math facts to learn!
Visualization Strategy
Students can visualize strategies to help them ‘see’ the math facts when using the Cotter Abacus. Let’s see how this works by considering 6 × 4, as shown below, using O’s and X’s.
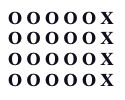
As you look at O’s on this array, you can see two sets of 10. You can also quickly see that there are 4 X’s, giving you a total of 24.
When using the Cotter Abacus, the student can also see the multiples of 9s. If they enter 9 × 3 on the abacus, they can see that 9 × 3 is the same as 10 × 3 – 3, giving a total of 27.
Using the O’s and X’s model similar to the Cotter Abacus format, let’s look at one final example: 7 × 7.
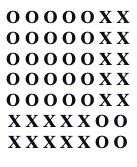
Here, we can see five rows of five O’s totaling 25. Looking at the X’s, we can see 20 more. Finally, we have 4 extra O’s on the bottom right, giving 25 + 20 + 4, or 49.
According to research, a student knows a math fact when they can answer it in 3 seconds or less. This amount of time gives the student time to process and use strategies to solve the problem.
Summary
Multiplication does not have to be a burden. When students are taught research-based strategies, such as visualization and using the commutative property, they successfully learn multiplication math facts.
The RightStart Math curriculum and RightStart Math Tutoring Multiplication and Division Book 1 use these strategies and more to ensure students understand and learn math.
Contact us to learn more!
